Anak-anakku yang hebat!
Jawablah pertanyaan berikut dengan cermat!
Dapatkah kamu menghitung berbagai bentuk pecahan?
Bagaimana cara kamu menghitung dengan cepat dan tepat?
Wow... sangat luar biasa.
Makin besar makin pintar,
pasti sungguh-sungguh belajar.
Belajar harus tekun dan sabar.
Anak-anakku kini yakinlah!
Belajar matematika menyenangkan.
Lakukan tugasmu dengan baik,
banyak-banyaklah membaca dan mengamati.
Berlatihlah mengomunikasikan.
Tentu kamu akan semakin mengerti.
Anak-anakku, ucapkan dengan semangat!
Belajar ... yes!
Matematika ... yes ... yes!
Prestasi ... yes ... yes ... yes!
Perkalian Pecahan Biasa dan Campuran beserta Contoh
Operasi perkalian pecahan sedikit berbeda dengan perkalian dengan bilangan desimal. Pada perkalian pecahan, pembilang dikalikan dengan pembilang dan penyebut dikalikan dengan penyebut pecahan yang dikalikan. Berikut dijelaskan mengenai operasi perkalian pecahan biasa dengan bilangan bulat, perkalian antar pecahan biasa, beserta perkalian pecahan campuran.
A. Cara Menghitung Perkalian Pecahan Biasa dengan Bilangan Bulat
Saat menghitung perkalian pecahan dengan bilangan bulat, yang dikalikan hanya pembilang dan bilangan bulat.
Contoh Soal:
Hasil 28/9 merupakan pecahan tidak biasa karena pembilang lebih besar dari penyebut. Sebaiknya diubah ke bentuk pecahan campuran yaitu 31/9.
Tips: untuk mengubah pecahan tidak biasa ke pecahan campuran, dapat dilakukan dengan pembagian bersusun.
Hal ini bersesuaian dengan definisi pecahan sebagai pembagian
a/b = a : bSehingga diperoleh 28/9 = 31/9
B. Cara Menghitung Perkalian Antar Pecahan Biasa
Menghitung perkalian antar pecahan biasa, dilakukan dengan mengalikan pembilang dengan pembilang dan penyebut dengan penyebut.
Contoh Soal:
Catatan: hasil akhir dapat disederhanakan jika memungkinkan, salah satunya dengan membagi pembilang dan penyebut dengan FPB-nya.
C. Cara Menghitung Perkalian Pecahan Biasa dengan Pecahan Campuran
Untuk menghitung hasil kali pecahan biasa dengan pecahan campuran dapat dilakukan dengan metode distributif.
x/y × (qa/b) = x/y × (q + a/b) = (x/y × q) + (x/y × a/b) = d
Contoh Soal:
Kemudian dilanjutkan dengan menjumlahkan masing-masing distribusi.
Nilai 20/14 dapat diubah menjadi 16/14, kemudian disederhanakan lagi menjadi 13/7.
D. Cara Menghitung Perkalian Antar Pecahan Campuran
Untuk menghitung hasil kali antar pecahan campuran juga dapat dilakukan dengan metode distributif. Hanya, saja bentuk distributif lebih panjang dari sebelumnya.
(pa/b) × (qc/d) = (p + a/b) × (q + c/d) = (p × q) + (p × c/d) + (a/b × q) + (a/b × c/d) = d
Contoh Soal:
Kemudian dapat diterapkan sifat komutatif, untuk menjumlahkan bilangan bulat dan pecahan.

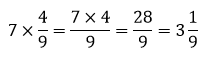
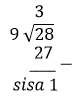
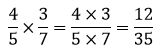
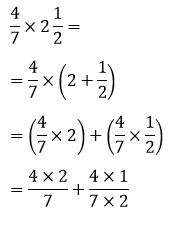
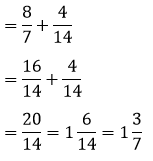
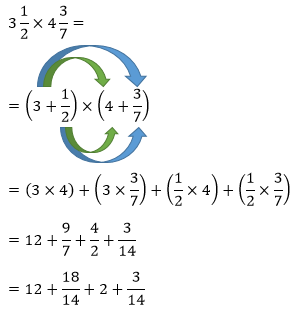
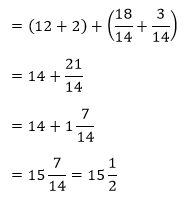
No comments:
Post a Comment